Come fare un disastro senza rendersene conto I metodi d'integrazione numerica sono quelli che permettono il calcolo degli integrali definiti di una funziona usando i calcolatori elettronici. Detto in maniera più accessibile (anche se non del tutto formalmente corretta), l'integrazione numerica è quel processo che conduce alla valutazione, in molti casi approssimata, dell'area compresa tra… Continua a leggere Integrazione numerica
Tag: matematica
10 milioni per 7 è sempre pari a 70 milioni?
Il calcolo numerico può condurre a sottili e pericolosi errori di arrotondamento. Per evitarli è necessario conoscere il problema e sapere come aggirarlo. Consideriamo il seguente programma, scritto in C: #include <stdio.h> int main() { float x = 7; float S = 0; int i; for (i = 0; i < 10000000; i++) { S… Continua a leggere 10 milioni per 7 è sempre pari a 70 milioni?
La bellezza salverà la fisica
Parafrasando la celebre massima di Dostoevskij (o forse, meglio, del suo "idiota"), in questo post discutiamo il ruolo della bellezza delle equazioni della fisica. Sì, lo so. Non tutte le leggi della fisica sono belle e molti lettori potrebbero non essere d'accordo con una tale affermazione. Tuttavia, dubito che la maggior parte di coloro che… Continua a leggere La bellezza salverà la fisica
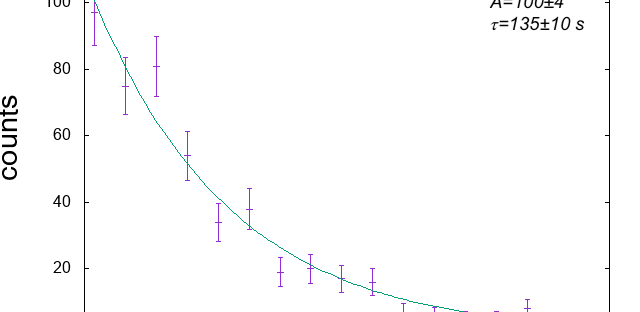
Esperimenti radioattivi
Con il simulatore di Geiger presentato nell'ultimo post si possono solo fare dimostrazioni qualitative circa la maniera in cui si comporta un rivelatore di particelle quando si avvicina una sorgente radioattiva. Al più si può fare una serie di misure che permettono di stabilire la legge secondo la quale il numero di conteggi per unità… Continua a leggere Esperimenti radioattivi
Le scuole di Fisica con Arduino e Smartphone crescono
Le Scuole di Fisica con Arduino e Smartphone cui ho dato vita dal 2016 continuano a riscuotere un discreto successo. Alcuni insegnanti hanno già iniziato a lavorare con Arduino nelle loro classi e presumibilmente avremo materiale da presentare al prossimo Congresso della Società Italiana di Fisica. Recentemente è stato pubblicato un mio post su Math is… Continua a leggere Le scuole di Fisica con Arduino e Smartphone crescono
La stima di π
Come stimare il valore di pi greco con @Scratch nel giorno del #piday
La Fisica non è un’opinione
"La Fisica non è un'opinione" è il titolo di un incontro-scontro con insegnanti (per lo più laureati in matematica) sul rapporto tra la matematica e la fisica. L'incontro si è tenuto il 10 febbraio 2017 presso il Dipartimento di Matematica di Sapienza, nell'ambito delle iniziative del Piano Lauree Scientifiche. Il mio esordio è stato abbastanza… Continua a leggere La Fisica non è un’opinione