Il 29 settembre 2023 Andrea Fontana (@twittatore) posta il seguente quesito sul social che tutti chiamano ancora Twitter, benché il suo proprietario si ostini a pretendere che si chiami X. Il post è interessante perché permette di far vedere come la fisica Newtoniana sia tutto fuorché intuitiva, con buona pace di quelli che dicono che… Continua a leggere Il dito di Archimede
Tag: fisica
The Best New Smartphone Book
I am very proud to announce that my book, "Physics Experiments with Arduino and Smartphones", published by Springer, has been awarded as the Best New Smartphone Books by BookAuthority.org, as announced in late 2021. BookAuthority collects and ranks the best books in the world, and it is a great honour to get this kind of… Continua a leggere The Best New Smartphone Book
La scuola di Bedonia
Dal 6 all'8 settembre 2021 si è svolta una nuova edizione della Scuola di Fisica con Arduino, questa volta in versione residenziale, con tutor e partecipanti ospitati dal Seminario Vescovile di Bedonia. La scuola è stata organizzata dall'Università di Parma sotto la direzione della Prof.ssa Maura Pavesi. Le attività si sono svolte nel modo classico:… Continua a leggere La scuola di Bedonia
Uno studio sperimentale della fisica dei gas
In uno dei miei ultimi post, mostro come ottenere dati sperimentali da Arduino tramite BLE. Come promesso, discuto ora la raccolta e l'interpretazione di questi dati, nel caso di un esperimento in cui un gas è soggetto a una trasformazione isòcora: un processo in cui la pressione p e la temperatura T possono cambiare, mentre… Continua a leggere Uno studio sperimentale della fisica dei gas
Come sembrare un genio
La relatività generale è una delle teorie tecnicamente più difficili, perché richiede conoscenze e abilità matematiche non comuni. Tuttavia, è possibile calcolare con buona precisione gli effetti relativistici indotti dalla curvatura dello spazio-tempo e persino ricavarne la formula con pochissimi, semplici, argomenti. Sappiamo dalla relatività ristretta che in un sistema che si muove rispetto a… Continua a leggere Come sembrare un genio
Il concetto di flusso: un esperimento
Il flusso di un campo vettoriale è definito come il vettore campo moltiplicato scalarmente per un vettore perpendicolare alla superficie rispetto alla quale si calcola. Il prodotto scalare, come noto, si calcola sommando i prodotti delle componenti omologhe dei due vettori. Per esempio, il prodotto scalare dei vettori A=(a, b, c) e B=(x, y, z)… Continua a leggere Il concetto di flusso: un esperimento
È uscito “Fisica con Arduino”
È in distribuzione da oggi il volume "Fisica con Arduino" da Zanichelli editore. Si tratta di un manualetto per le scuole superiori nel quale s'introduce la programmazione di Arduino attraverso lo studio sperimentale di problemi di fisica. Come amo dire spesso, nei miei libri di argomenti legati all'informatica e alla programmazione, non troverete mai il… Continua a leggere È uscito “Fisica con Arduino”
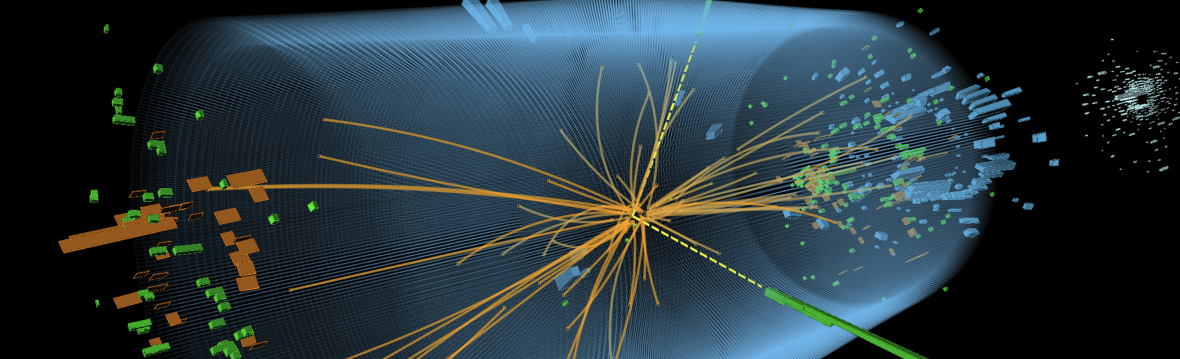
Il meccanismo di Higgs
Se si ha una conoscenza, anche solo elementare, della fisica, è molto probabile che non si sia soddisfatti delle spiegazioni metaforiche del ruolo del bosone di Higgs nel "dare massa alle altre particelle". In fondo, non spieghiamo la gravità e l'elettromagnetismo usando metafore. Di solito scriviamo equazioni il cui significato è molto chiaro e preciso,… Continua a leggere Il meccanismo di Higgs
Come si affronta un esercizio di fisica
Praticamente tutti i libri di esercizi di fisica che ho (gli editori me ne mandano ogni tanto in visione) sono tutti uguali: cambia solo l'insieme degli esercizi. Lo stesso esercizio, in effetti, si può vestire in modo diverso e dunque anche loro non sono poi così diversi: che so, in un esercizio di cinematica a… Continua a leggere Come si affronta un esercizio di fisica
La distribuzione di Fermi-Dirac
Enrico Fermi divenne famoso, nella comunità dei fisici del tempo, per aver pubblicato, nel 1926, un articolo nel quale calcolava la distribuzione in energia delle particelle identiche con spin semintero. Nello stesso anno, ma poco più tardi, anche Paul Dirac arrivò indipendentemente allo stesso risultato e per questo la distribuzione si chiama oggi di Fermi-Dirac.… Continua a leggere La distribuzione di Fermi-Dirac